
总的来说还行,笔试做的很好,很流畅的就做了,机试做得稀烂。拿了三个奖状,一个参与奖(所有人都有哈哈),一个总分优秀(其实就是二等,8 ~ 24 名),一个是笔试优异(其实就是一等)。
笔试做到了全场 Rank 1!我很开心,但是其实笔试的题真没啥难的。大佬都看不上 NJU 所以肯定都没来,我就捡了个漏,好耶。
机试有一些阴间题也有好题。完全不适应 3 个小时 3 道题。两天都没上 100,导致最后总分就二等。实际上每天会做的题都有 150 分左右,但是就是没写出来或者忘了(呃呃)。
下面我会给每天的题意(简述),正解(如果知道)。
主要是你能不能读懂题,因为它不给任何术语定义。然后证明过程应该就不是很难了。我考的时候不知道同构是什么,尴尬了。
设
为长度为 的置换构成的群, 为长度为 的偶置换构成的群,证明 和 同构。
我还没仔细想,大伙来做吧。
我切了,哈哈,简单吧。
有一个无限集合
上面定义了一个偏序。证明 要么存在一个无限子集元素两两可比要么存在一个无限子集元素两两不可比。
首先两两可比就是链,两两不可比就是反链。
反证,假如
一个直觉的证明就是用 Dilworth 定理,最长反链等于最小链覆盖。用有限条有限长度的链就能覆盖整个集合,那么这个集合是有限集合,与题意矛盾。
但是这样做是假的。因为 Dilworth 不能用在无限集合上。改进也不难。设最长链大小是
场上本来不会的,但是莫名其妙会了。其实我和通常解法不太一样。我想了个经典知名神奇函数就过了。
设
为一个定义在正实数集上的函数,并且函数值恒为正实数,有 。 请问如下命题是否恒成立?如果是,请证明;如果不是,请给出对应的
。 命题:对于任意正实数
, 。
不成立。
官方题解:
场上的一个其他题解:
我的做法:
比较简单一个题。
给定一个二部图
,保证 中每个点的度数为 。定义一个“输入”为对 中每个点赋非负整数权值的方案。对于一个输入, 中点的权值为它邻居的权值和除以 的余数。定义“输出” 为 中每个点的权值构成的序列。 证明:若有一个输入
导致输出为 ,必有一个输入 也导致输出为 ,且 中 的个数大于等于一半。
记一个输入
将
所以,只需令
我为啥跳掉这题啊……
给定
个长度为 的小写字母字符串,再给出一个极限距离 ,请问是否有一个长度为 的任意字符串,满足到每个给定字符串的汉明距离不超过 。如果有请输出这个串,否则输出 。 两个字符串
的汉明距离 定义为 。 多测,最多
组, 。
先删去所有字符串都相同的位置,若剩下的串长度大于
将第一个串作为初始答案串
注意到如果搜索层数超过
致敬传奇题目 P4117,但我就是忘了(呃呃),导致只会
给定一个序列
,每次询问 ,求出以下过程的结果: int f(int l, int r, int v) { int cnt = 0 for (int i = l; i <= r; i++) { if (v >= a[i]) { v -= a[i]; cnt++; } } return cnt; }
。
分块,对每块求出,对于每个
然后就是 P4117 的做法就行了。
听说有
比较智慧的交互题,次数限制放得还挺宽松,唯一的缺点就是我不会 :(
有一个长度为 1000 的隐藏 01 串需要你在 256 次询问内猜出来。每次你可以问一个 01 串,交互器会返回两个串的汉明距离。
戏剧化题意:你有 1000 道选择题,你每次交卷系统都会给你打分,系统限制交卷 256 次。请你无脑 AK 这套题。
看图吧。


T1:不会,场上唯一做出来的人单独拿了个奖,这就是这题的含金量吗。
T2:没想,有不少人做出来了,但我去冲 T1 了。What can I say?
T3:随便写了个结果就对了。What can I say?
看图吧,话说我放出来这个应该没有问题吧,有的话给我说,我改。


开头就得说一句 T3 逆天。我对这场完全没啥话说。。。
反射容斥板子,一模一样,想看上网查“反射容斥”随便找个文章,里面的例题估计都这个。
我不会,忘了题意了。。。
What can I say? 出题人透露此题没有验题人通过,这也不重要,反正致敬传奇题目 この問題はほんとうにひどい問題であるため,できれば先に他の問題のほうをお楽しみいただければと思っておりまして,ですので他の問題を通し終えて暇になり,かつその暇を。感觉比这个还抽象。
给定一张黑白颜色的图片,用 01 表示黑白。这个图片是人以画圈圈为目标画出的图。请你识别这个图中有几个圈圈。保证画画的人画的目标一定是一个或者两个圈。
时间限制 10 s,好吧,不如比赛时间 2 h 45 min。其实还是看图更好。


以下是一些灵魂样例:



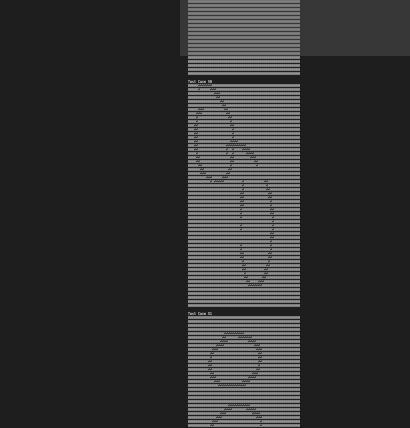

搞笑的画手!